BFS
Breadth-First Search
BFS는 주로 무방향 그래프에서 사용되는 그래프 탐색 알고리즘으로 넓이 우선 탐색 이라고 불린다.그래프를 순회하거나 최단경로(Shortest Path)를 구할때도 사용한다.구현할때는 Queue를 사용한다.
Shortest Path Problem
최단 경로를 구하는 문제이다.

예를 들어 위의 그래프에서 s에서 b까지 가는 가장 최단거리는 <s,b>이다.
우선 주어진 그래프 G = (V,E)에서 BFS 알고리즘의 리턴값은 d[v](s to v 까지의 거리),pred[v](전에 지나온 노드)이다.
pred[v]는 최단거리를 위해 실제로 지나온 노드를 기록하기에 경로를 찾을 수 있다.따라서 BFS가 그래프 탐색을 완료하면 이를 바탕으로 최단 경로 트리(Shortest path tree)를 만들 수 있다.
BFS example
우선 주어진 그래프 G가 인접 리스트(Adjacency list)로 구현되었다 가정하고 방문한 노드의 인접한 정점은 Gray로 표현되고 방문한 노드는 Black 나머지는 White로 표현된다 할때.모든 정점을 순회하는 BFS의 의사코드는 다음과 같다.(초기화 과정은 생략된 상태)

그랬을때의 정점을 나타낸 표와 그래프는 다음과 같다고 가정하자.
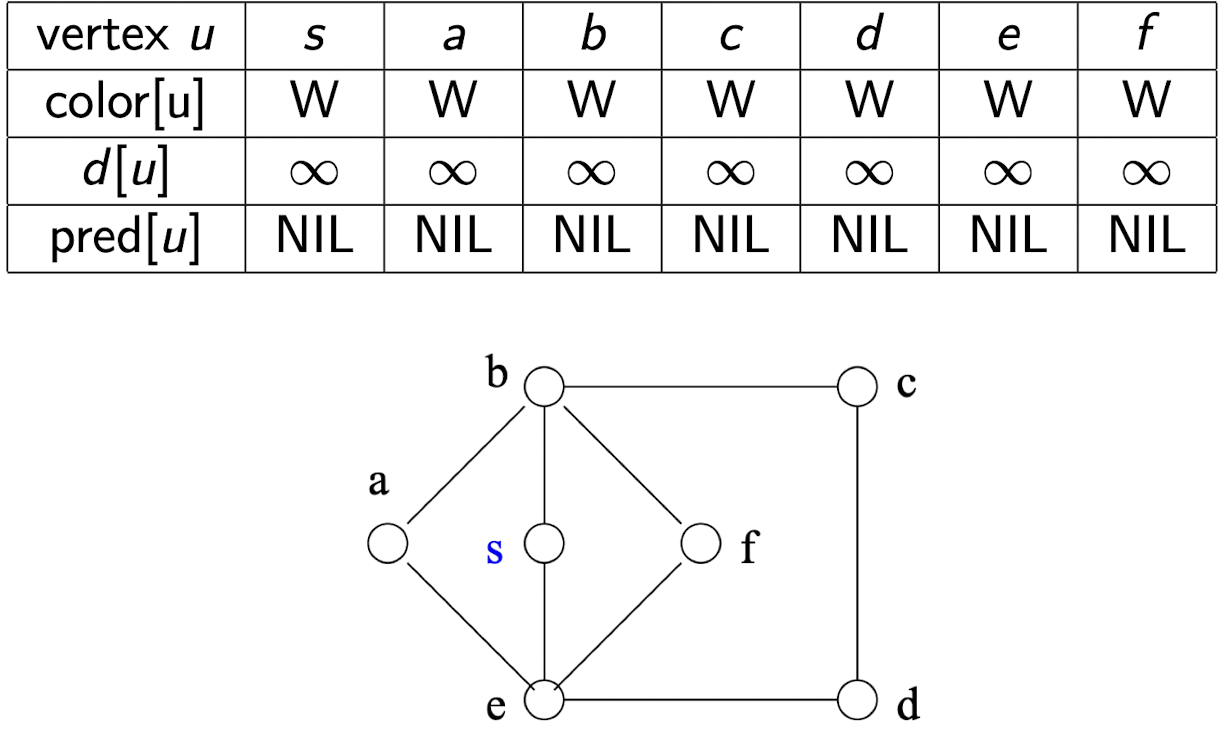
처음 S를 방문하면 다음과 같은 상태로 변한다.

S를 방문하고 방문한 노드와 인접노드의 상태를 변화시켰다.이때 큐에는 b,e가 enqueue되고 테이블은 다음과 같이 변화한다.
이때 사실 b,e가 들어가는 순서는 중요하지 않다.둘 중 아무거나 들어간다.
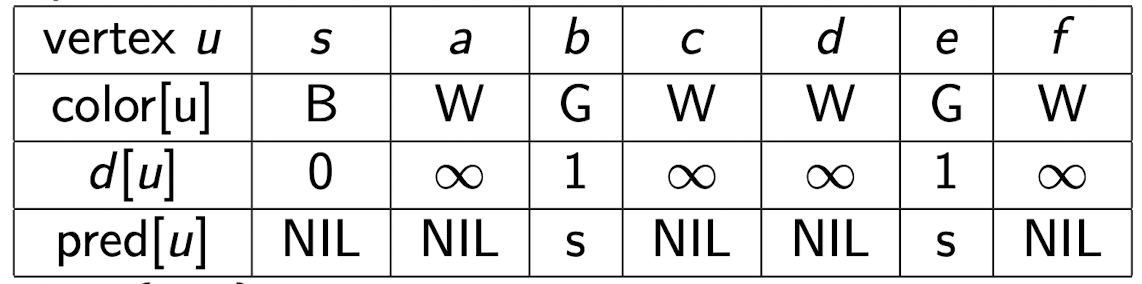
이후 b를 dequeue하고 b를 방문처리한후 b의 인접노드 상태를 변화시킨다.이후 큐에 a,c,f를 enqueue한다.

테이블은 다음과 같이 변화한다.

이를 반복하면 모든 정점을 반복하게 되고 그 순간은 queue가 비었을때이다.
최종적으로 테이블은 이렇게 바뀐다.

이로서 최단거리와 pred[u]를 통해 최단 경로도 구할 수 있다.
Analysis BFS

BFS의 알고리즘의 핵심은 큐가 빌때까지 계속반복하면서 방문한 노드를 dequeue하면서 해당 노드의 인접 노드를 enqueue하는 것이다.
반드시 방문 처리를 해야 무한 루프가 발생하지 않는다.
분석을 위해 각 정점의 갯수를 n으로 간선의 갯수를 e라 하고 각 연산은 상수시간이 걸린다 했을때.초기화에는 3n + 3의 단위시간이 소요되다.색 초기화,거리 초기화,선행자 초기화가 n번씩 3번 수행되고 초기 작업 3번이 수행되기 때문이다.정점 및 간선 처리에서는 5 * deg(u)(각 정점의 차수 + 2)가 소요된다.dequeue연산,순회하면서 색 상태 확인,상태 변경,거리 갱신,선행자 갱신,enqueue연산이 필요하며 v의 상태를 B로 변경하는 연산 1이 소요되기 때문이다.근데 그래프의 모든 간선을 정확히 한 번씩 확인하기에 정점의 차수는 2e가 되며 따라서 10e + 2n이 된다.총 시간복잡도는 이를 더한 9n + 2e - 1으로 시간복잡도는. O(n+e)로 선형시간이 걸림을 확인할 수 있다.
비연결 그래프에서의 BFS 적용
우선 그래프에서의 컴포넌트(Component)를 알아야한다.컴포넌트는 그래프의 정점들 중 서로 연결된 정점들의 최대 집합으로,각 컴포넌트는 내부적으로 모든 정점이 경로로 연결되어 있지만 다른 컴포넌트와는 분리된 상태를 의미한다.
비연결 그래프(non-connected graphs)는 그래프의 모든 정점이 하나의 연결 컴포넌트로 연결되지 않는 그래프를 의미한다.
BFS는 시작 정점으로부터 연결된 컴포넌트만 탐색한다.따라서 다른 컴포넌트에 속한 정점은 거리가 무한대로 표기된다.따라서 BFS를 그래프의 모든 정점에 대해 반복 수행해서 각 컴포넌트에 대해 별도의 트리를 생성한다.이는 포레스트(Forest)를 리턴한다.
아래는 그에 대한 수도 코드이다.

BFS의 정확성은 귀납적으로 증명이 가능하고 최단거리는 귀류법으로 증명이 가능하다.