점화식,재귀 트리,마스터 정리
점화식(Recurrences)
점화식은 알고리즘의 실행 시간을 문제 크기와 부분 문제에 따라 표현하는 방법으로 분할 정복 알고리즘(Divide-and-Conquer Algorithm)을 분석하는 데 중요하다.점화식은 재귀 관계를 나타낸다.
재귀 트리(Recursion Tree)
재귀 트리는 알고리즘이 재귀적으로 호출되는 과정을 시각적으로 모델링한 것으로 재귀 호출을 트리 형태로 표현하여 직관적으로 분석하기 쉽게 하는 것이다.일반적으로 알고리즘의 성능을 정밀하게 계산하기 위해서는 점화식을 이용한 수학적 귀납법으로 결과를 도출하지만 재귀알고리즘은 이를 적용하기 어렵기에 효과적이다.
예를 들어보면 다음과 같다.

이 식에 대해서 재귀트리를 그려보면 다음과 같다.

재귀 트리의 각 레벨의 작업량을 다 더하면 전체 작업량이 나오고 이를 통해 시간복잡도를 계산할 수 있다.
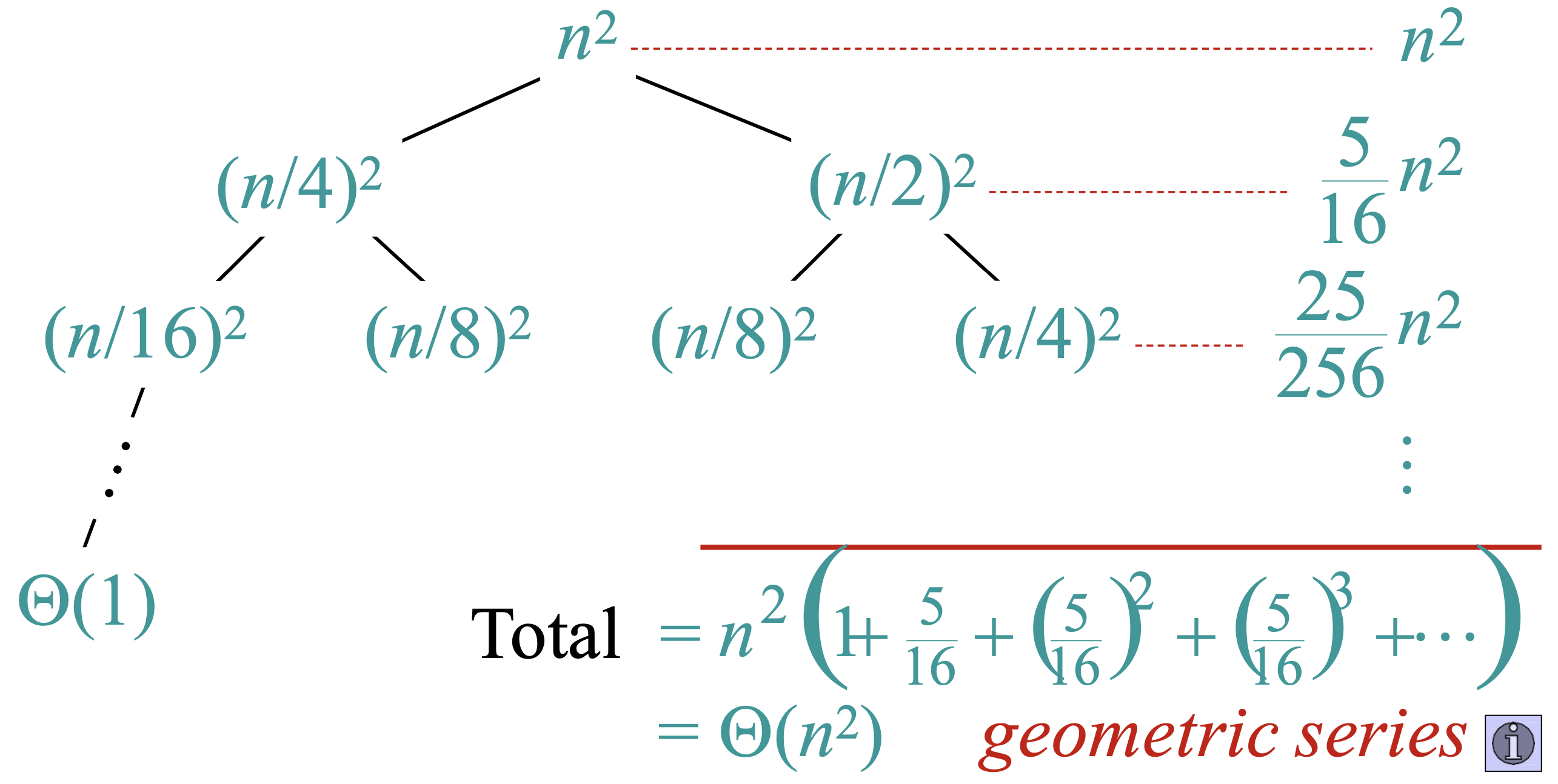
결국 등비수열 부분합의 극한인 등비급수로서 표현이 가능하다.
마스터 정리(Master Theorem)
마스터 정리는 재귀 관계의 점화식을 분석해 시간 복잡도를 도출하는데 사용되는 강력한 도구다.
마스터 정리는 크게 3가지로 나뉜다.
대부분의 재귀 관계의 꼴은 다음과 같다.

이때의 조건은 a가 1보다 크거나 같고 b가 1보다는 크고 함수 f는 양의 함수 일때다.
a는 분할한 부분 문제의 수,b는 입력의 크기가 줄어드는 비율,함수 T는 부분 문제 해결 시간,함수 f는 병합에 필요한 시간을 의미한다.
이를 재귀 트리형태로 나타냈을때 리프의 노드의 차수가 같을때를 의미한다.
이 꼴을 만족하는 알고리즘으로는 대표적으로 병합 정렬이 있다.물론 마스터 정리가 모든 케이스에 적용되지는 않지만 대부분의 점화식에는 적용이 된다.
우선 함수 f를 기준 함수(watershed function)로 정의하자.

그리고 일반화된 재귀 트리는 다음과 같다.

이 그림을 통해서 기준 함수가 어떻게 유도 됬는지 확인할 수 있다.
이제 케이스들을 확인해보자
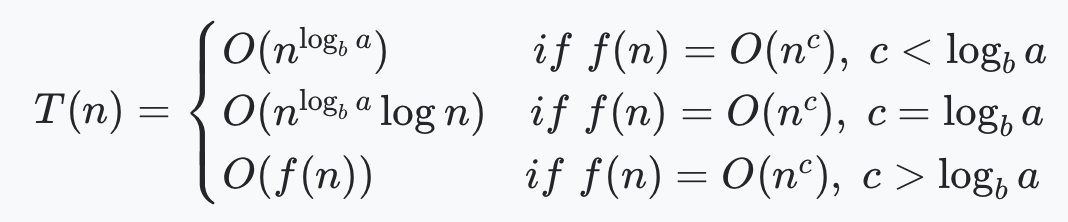
어디에 가중치가 더 많으냐에 따라 케이스를 나눌 수 있다.
1.함수 T의 소요시간이 가중치가 높을때

2.함수 T,F의 가중치가 동일하거나 균형이 맞을때

3.함수 F의 소요시간이 가중치가 더 높을때

즉,이 정리를 활용하기 위해서는 f(n)의 값과 기준함수값을 비교해서 케이스를 적용하는 것이다.